In mathematics, the root mean square (abbreviated RMS or rms), also known as the quadratic mean, is a statistical measure of the magnitude of a varying quantity. It is especially useful when variates are positive and negative, e.g., sinusoids. In the field of electrical engineering, the effective (RMS) value of a periodic current is equal to the DC voltage that delivers the same average power to a resistor as the periodic current.[1]
It can be calculated for a series of discrete values or for a continuously varying function. Its name comes from its definition as the square root of the meanof the squares of the values. It is a special case of the generalized mean with the exponent p = 2.
Definition[edit]
The RMS value of a set of values (or a continuous-time waveform) is the square root of the arithmetic mean (average) of the squares of the original values (or the square of the function that defines the continuous waveform).
In the case of a set of n values 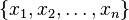 , the RMS
, the RMS
The corresponding formula for a continuous function (or waveform) f(t) defined over the interval 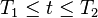 is
is
and the RMS for a function over all time is
The RMS over all time of a periodic function is equal to the RMS of one period of the function. The RMS value of a continuous function or signal can be approximated by taking the RMS of a series of equally spaced samples. Additionally, the RMS value of various waveforms can also be determined withoutcalculus, as shown by Cartwright.[2]
In the case of the RMS statistic of a random process, the expected value is used instead of the mean.
'오디오 음성' 카테고리의 다른 글
| 파스칼 (단위) (0) | 2015.07.09 |
|---|---|
| 롬바드 효과 (Lombard Effect) (0) | 2015.06.18 |
| Equal-loudness contour (등청감 곡선) (0) | 2014.06.18 |
| Absolute threshold of hearing (최소 가청값, 최소 가청치) (0) | 2014.06.18 |
| Sound Pressure Level (SPL) (0) | 2014.06.18 |


![f_{\mathrm{rms}} = \sqrt {{1 \over {T_2-T_1}} {\int_{T_1}^{T_2} {[f(t)]}^2\, dt}},](http://upload.wikimedia.org/math/1/8/d/18d7849093bc289403a534d37cd20838.png)
![f_\mathrm{rms} = \lim_{T\rightarrow \infty} \sqrt {{1 \over {T}} {\int_{0}^{T} {[f(t)]}^2\, dt}}.](http://upload.wikimedia.org/math/0/3/8/03818626990ed332916202cfaa40400c.png)